Meridiane su Internet |
| Per una rassegna completa clicca qui |
"L'ora solare" è ancorata all'idea che quando il sole raggiunge il suo punto più alto (quando attraversa il meridiano), è mezzogiorno e, il giorno successivo, quando il sole attraversa di nuovo il meridiano, sarà di nuovo mezzogiorno. Il tempo che è trascorso fra due mezzogiorni successivi è talvolta maggiore e talvolta minore di 24 ore del tempo dell'orologio. Nei mesi centrali dell'anno, la lunghezza del giorno è abbastanza vicina alle 24 ore, ma intorno al 15 Settembre i giorni sono lunghi solo 23 ore, 59 minuti e 40 secondi mentre intorno a Natale, i giorni durano 24 ore e 20 secondi.
"L'ora dell'orologio" è ancorata all'idea che ciascun giorno è lungo esattamente 24 ore. Questo non è esattamente vero, ma è ovviamente molto più conveniente avere un "sole medio" che impiega esattamente 24 ore ogni giorno, in quanto gli orologi meccanici, e, più recentemente, quelli elettronici possono essere costruiti in modo da misurare questi intervalli di tempo uguali.
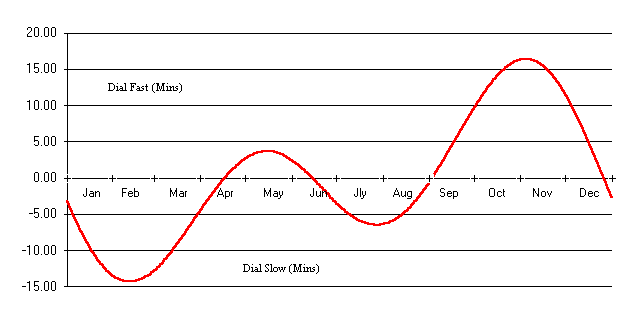
Ovviamente, queste piccole differenze nella lunghezza dei "giorni solari" e dei "giorni medi" producono differenze maggiori fra "l'ora solare" e "l'ora dell'orologio". Queste differenze raggiungono un picco di oltre 14 minuti a metà Febbraio (quando il "tempo solare" è più lento del "tempo dell'orologio") ed oltre 16 minuti all'inizio di Novembre (quando il "tempo solare" è più veloce del "tempo dell'orologio"). Ci sono anche due picchi minori a metà Maggio (quando il "tempo solare" è circa 4 minuti più veloce) ed a fine Luglio (quando il "tempo solare" è oltre 6 minuti più lento) (Questi picchi minori hanno un effetto fortunato, infatti nell'emisfero settentrionale, le differenze sono relativamente minori durante la maggioranza di mesi in cui si ha una ragionevole durata dei periodi di sole).
Le differenze non si accumulano nel corso degli anni, in quanto il "tempo dell'orologio" è stato progettato in modo che, ogni quattro anni, viene inserito un anno bisestile e i due tipi di tempo ritornano così molto vicini al valore di partenza. (Si dice "molto vicini" poiché il "tempo dell'orologio" deve essere ancora aggiustato in modo da non avere un anno bisestile il primo anno del secolo, eccetto quando l'anno è esattamente divisibile per 400, per cui il 1900 non è stato un anno bisestile, ma il 2000 sì). Nonostante questa correzione, recentemente è stato aggiunto un secondo extra al "tempo dell'orologio".
I motivi di queste differenze vengono discusse di seguito, seguite da alcune informazioni su come sono tali differenze in certi periodi dell'anno.
Queste differenze derivano da due cause piuttosto diverse. La prima è che il piano dell'Equatore non è lo stesso piano dell'orbita della Terra attorno al Sole, ma è spostato da esso dell' angolo di obliquità.
La seconda è che l'orbita della Terra attorno al sole è un'ellisse e non un cerchio, ed il movimento apparente del sole non è perciò esattamente uguale durante l'intero anno. Il sole sembra muoversi più velocemente quando la Terra è più vicina al sole.
Questi due effetti vengono spiegati in maggior dettaglio in un opuscolo del Royal Greenwich Observatory ed in un eccellente articolo di Art Carlson's alla fine di questa pagina.
La somma dei due effetti costituisce l'Equazione del Tempo, che è la curva rossa con i suoi caratteristici picchi gemelli mostrata di seguito. (Molti ringraziamenti a Patrick Powers per aver fornito questo grafico sundial page).

Alcune persone preferiscono questa informazione presentata come tabelle invece che come grafici, per cui due tabelle vengono presentate di seguito per tua informazione. Queste sono entrambe due utili tabelle riassuntive, che ti forniranno una diversa visione dell'Equazione del Tempo, e che ti possono aiutare a ricordare alcune caratteristiche chiave, ad esempio, che fra la fine di Marzo e metà Settembre il sole non si allontana mai più di 6 minuti dal "tempo dell'orologio", e per tutto Febbraio è 13 o 14 minuti più lento! Se vuoi conoscere l'Equazione del Tempo per ciascun giorno dell'anno, c'è una tabella nell'Appendice A del libro di Waugh.
La tabella mostra le date in cui il "Tempo Solare" è (quasi)
esattamente un
dato numero di minuti più veloce o lento del "Tempo
dell'orologio"
Minuti
Veloce
16 Nov 11 Ott 27
15 Nov 17 Ott 20
14 Nov 22 Ott 15
13 Nov 25 Ott 11
12 Nov 28 Ott 7
11 Dic 1 Ott 4
10 Dic 4 Ott 1
9 Dic 6 Set 28
8 Dic 9 Set 25
7 Dic 11 Set 22
6 Dic 13 Set 19
5 Dic 15 Set 16
4 Dic 17 Set 13
3 Dic 19 Mag 4 Mag 27 Set 11
2 Dic 21 Apr 25 Giu 4 Set 8
1 Dic 23 Apr 21 Giu 9 Set 5
0 Dic 25 Apr 15 Giu 14 Set 2
1 Dic 28 Apr 12 Giu 19 Ago 29
2 Dic 30 Apr 8 Giu 23 Ago 26
3 Gen 1 Apr 5 Giu 29 Ago 22
4 Gen 3 Apr 1 Lug 4 Ago 18
5 Gen 5 Mar 29 Lug 9 Ago 12
6 Gen 7 Mar 26 Lug 18 Ago 4
7 Gen 9 Mar 22
8 Gen 12 Mar 19
9 Gen 15 Mar 16
10 Gen 18 Mar 12
11 Gen 21 Mar 8
12 Gen 24 Mar 4
13 Gen 29 Feb 27
14 Feb 5 Feb 19
Eq. tempo per il: 5 15 25 Camb. medio (sec) Gennaio -5m03 -9m10 -12m12 20 Febbraio -14m01 -14m16 -13m18 5 Marzo -11m45 -9m13 -6m16 16 Aprile -2m57 +0m14 +1m56 18
Maggio +3m18 +3m44 +3m16 4 Giugno +1m46 -0m10 -2m20 16 Luglio -4m19 -5m46 -6m24 20 Agosto -5m59 -4m33 -2m14 11
Settembre +1m05 +4m32 +8m04 20 Ottobre +11m20 +14m01 +15m47 13 Novembre +16m22 +15m28 +13m11 10 Dicembre +9m38 +5m09 +0m13 27
La rotazione della Terra è un buon orologio poiché è, per scopi pratici, costante. Naturalmente, gli scienziati non sono pratici e prestano attenzione al fatto che la lunghezza del giorno aumenta di un secondo ogni 40 000 anni. Per il resto di noi, si tratta solo di trovare un metodo conveniente per determinare dove è rivolta la Terra. Le stelle potrebbero essere un buon metodo, ma sono troppo flebili (e troppe) la notte e scompaiono durante il giorno. Un utile aiuto potrebbe essere il Sole, che splende durante il giorno ed è difficile da trascurare. Purtroppo, la posizione apparente del sole è determinata non solo dalla rotazione della Terra attorno al proprio asse, ma anche dalla rivoluzione della Terra attorno al Sole. Vorrei spiegare esattamente come funziona questa complicazione, e come trattarla.
Il diametro del Sole visto dalla Terra è di1/2 grado, per cui si muove di una quantità pari al suo raggio ogni minuto.
24ore 60min 1 ------ x ----- x - grad = 1min 360gr 1ora 4Ciò significa che è difficile leggere una meridiana con una approssimazione migliore del minuto, e quindi non è neppure necessario regolare i nostri orologi con una precisione maggiore. Sfortunatamente, se noi definiamo il secondo essere costante (cioè, la frazione 1/31 556 925.974 7 dell'anno 1900, il "secondo efemeride"), allora troveremo alcuni giorni (da mezzogiorno a mezzogiorno) con più di 86,400 secondi, ed alcuni con meno. Il giorno solare del Natale, ad esempio, è lungo 86,430 secondi. La discrepanza fra il "tempo apparente" ed il "tempo medio" può arrivare fino a +/- 15min. Da cosa deriva ciò?
1gio 24ore 60min --- x ----- x ----- = 3min 56sec 366 1gio 1oraIl problema deriva dal fatto che 3min 56sec sono solo un valore medio. Pensate ad un osservatore seduto al polo nord su una piattaforma che ruoti completamente ogni 23ore 56min 4sec. Egli vedrà ferme le stelle ed il sole muoversi in circolo. Il piano di questo cerchio è detto "eclittica" ed è inclinato di 23.45gradi rispetto al piano dell'equatore. L'osservatore vedrà il sole salire dall'orizzonte fino a 23.45gradi, e poi riscendere sull'orizzonte. Il sole si muoverà a velocità costante (sto mentendo, ma aspettate ancora un po') lungo il suo cerchio, ma l'ombra proiettata dal Polo Nord (quello con le strisce bianche e rosse) non si muoverà a velocità costante. Quando il sole è vicino all'orizzonte, esso deve salire ad un angolo di 23.45gradi, per cui si deve muovere di1.09gradi prima che l'ombra si sposti di1grado.
1grad
------------- = 1.0900grad
cos(23.45grad)
D'altra parte, a metà estate, il sole è alto nel cielo e
prende una scorciatoia, per cui si deve muovere solo di 1grado lungo il suo
cerchio per far muovere la sua ombra di 1.09gradi.
Questo effetto può essere generalizzato ai climi più
temperati, per cui in primavera ed autunno avremo un valore di 3min 56sec,
mentre in estate ed inverno sarà corrispondentemente aumentato a 4min
17sec.
Quindi una meridiana può guadagnare o perdere fino a 20sec/giorno a
causa dell'inclinazione dell'eclittica, in base al periodo dell'anno.
Se un giorno la meridiana è precisa, sei settimane più tardi
può avere accumulato un errore massimo di10min.
20sec 2 1min
----- x 45gio x -- x ----- = 10min
1gio pi 60sec
La correzione stagionale è nota come "equazione del tempo" e deve
ovviamente essere tenuta di conto se vogliamo una meridiana esatta al
minuto.
Se lo gnomone (l'oggetto che proietta l'ombra) non è un'estremità ma è un punto (es., un foro), l'ombra (o il punto luminoso) traccerà una curva durante il corso del giorno. Se l'ombra viene proiettata su di una superficie piana, questa curva sarà (di solito) una iperbole, poiché il circolo del moto solare insieme alla punta dello gnomone definiscono un cono, ed un piano interseca un cono con una sezione conica (iperbole, parabola, ellisse, o cerchio). Agli equinozi, il cono degenera in un piano e l'iperbole in una linea. Con un'iperbole differente ogni giorno, i segni delle ore possono essere posti su ciascuna iperbole che include tutte le necessarie correzioni. Purtroppo, ciascuna iperbole corrisponde a due diversi giorni, uno nella prima metà ed uno nella seconda metà dell'anno, e questi due giorni richiedono differenti correzioni. Un compromesso conveniente è quello di tracciare una linea per il "tempo medio" ed aggiungere una curva che mostri la posizione esatta dell'ombra al mezzogiorno durante il corso dell'anno. Questa curva assumerà una forma ad 8 ed è nota come "analemma". Confrontando l'analemma con la linea media del mezzogiorno, possiamo determinare la correzione da applicare per quel giorno. All'equinozio, troviamo che il giorno solare è più vicino della media al giorno siderale, cioè, è più corto, per cui la meridiana va avanti. Ciò significa che in primavera ed autunno l'ora corretta sarà prima di quanto indicato dall'ombra, di una quantità data dalla curva. In estate ed inverno l'ora esatta sarà più tardi di quanto indicato.
3min 56sec
---------- x 0.034 = 8.0sec/gio
1gio
e nel corso di 3 mesi una meridiana accumula un errore di 8min a causa
dell'eccentricità dell'orbita terrestre.
8.0sec 2 1min
------ x 91gio x -- x ----- = 8min
1gio pi 60sec
Quindi l'ora esatta sarà più tardi di quando indicato
dall'ombra all'equinozio primaverile e prima all'equinozio autunnale.
Ciò fa spostare le date a cui la meridiana è precisa dagli
equinozi all'estate, rendendo il cerchio estivo della curva a forma di 8
più piccolo.
L'errore di 20sec/giorno dovito all'inclinazione dell'eclittica e quello di 8sec/giorno dovuto all'eccentricità hanno lo stesso segno intorno a Natale e si sommano esattamente (o meglio, quasi) per dare i 30sec/giorno ricordati precedentemente. Gli errori accumulati di10min ed 8min dovuti a questi due effetti non si sommano in maniera esatta, per cui l'errore massimo accumulato è leggermente inferiore ai18min. Calcolando tutto correttamente, si troverebbe che nel corso di un anno una meridiana potrà andare avanti fino a16min 23sec (il 3 Novembre) ed indietro fino a 14min 20sec (il 12 Febbraio).
Supponi, in Ottobre, di iniziare una pausa di lavoro di 15min alle10:45 dell'orologio. Se ti regoli con la meridiana all'esterno, senza tener conto dell'equazione del tempo, sarai già in ritardo per la sessione delle11:00 non appena esci dalla porta.
|
Questa pagina è stata tradotta dalla pagina Inglese da Guido
Flamini, Italia nel Marzo 2000.
This complete website © Internetworks, 1997-2007. The site was designed and is maintained Internetworks Ltd of Epsom, England |
| www.sundials.co.uk/equation.htm first posted 1996 last revision 25 April 1999 |
| Comments/ suggestions/ problems, please get in touch with the Webmaster |