Relojes de Sol en Internet |
|
Para una vista completa de este sitio oprima aquí |
Relojes de Sol en Internet - La Ecuación del Tiempo
"Hora solar" y "hora civil"
Los relojes de Sol indican la "hora solar". Los relojes comunes indican la "hora civil". Ninguno es "mejor" que el otro, cada uno tiene sus aplicaciones y ambos son útiles e interesantes.
El "tiempo solar" está relacionado con la idea de que cuando el Sol alcanza su punto más alto (cuando cruza el meridiano), es mediodía y al día siguiente, cuando el Sol vuelva a cruzar el meridiano, será mediodía una vez más. El tiempo que transcurre entre dos mediodías sucesivos algunas veces es mayor y otras veces menor de 24 horas. En los meses de mitad del año, la duración del día es muy cercana a 24 horas, pero alrededor del 15 de Septiembre, los días son de 23 horas, 59 minutos y 40 segundos, mientras que cerca de la Navidad los días son de 24 horas y 20 segundos de duración.
El "tiempo civil", está condicionado a días de 24 horas de duración. No es real que los días sean de 24 horas, pero es obvio que es más conveniente tener un "Sol medio" de exactamente 24 horas por día, porque pudieron construirse los relojes mecánicos y más recientemente los electrónicos, que miden esos intervalos de tiempo exactamente iguales.
Obviamente esas pequeñas variaciones en la duración de los "días solares" y los "días medios" van produciendo mayores diferencias entre el "tiempo solar" y el "tiempo civil". Estas diferencias alcanzan un máximo de poco más de 14 minutos a mediados de Febrero (cuando el "tiempo solar" es lento respecto al "tiempo civil") y poco más de 16 minutos al principio de Noviembre (cuando el "tiempo solar" es rápido respecto al "tiempo civil"). Existen también otras dos variaciones menores a mediados de Mayo (cuando el "tiempo solar" es más rápido aproximadamente 4 minutos) y a finales de Julio (cuando el "tiempo solar" es más lento, un poco más de 6 minutos). (Afortunadamente, en el hemisferio Norte las diferencias son relativamente menores durante la mayoría de los meses en que hay más días soleados).
Las diferencias no se acumulan a lo largo de los años, porque el "tiempo civil" se ha diseñado de tal manera que durante un ciclo de 4 años, incluyendo un año bisiesto, los tiempos civil y solar casi se igualan nuevamente. (Lo de "casi" se debe a que el "tiempo civil" todavía tiene que ajustarse por no tener un año bisiesto al final de cada siglo, excepto cuando el año es exactamente divisible por 400; así, el año 1900 no fue un año bisiesto, pero el año 2000 lo será). Aún con esta corrección, recientemente se añadió un segundo extra al "tiempo civil".
Las razones para estas diferencias se discuten más adelante, seguidas de más información acerca de las variaciones en determinadas fechas del año.
¿Porqué los días son de diferente duración?
Estas diferencias surgen por dos causas independientes. La primera es que el plano del Ecuador no es el mismo que el plano de la órbita de la Tierra alrededor del Sol, sino que está inclinado respecto de ella por lo que se conoce como el ángulo de oblicuidad.
La segunda razón es que la órbita de la Tierra alrededor del Sol es una elipse y no un círculo; por ello el aparente movimiento del Sol no es igual todo el año. El Sol parece moverse más rápido cuando la Tierra está mas cerca de él.
Estos dos efectos se explican con más detalle en la página del Real Observatorio de Greenwich y en el excelente artículo de Art Carlson al final de esta página.
La suma de los dos efectos es la Ecuación del Tiempo, representada en la curva de color rojo que se muestra enseguida. (Agradecemos a Patrick Powers por facilitar esta gráfica de su página personal de relojes de Sol.).
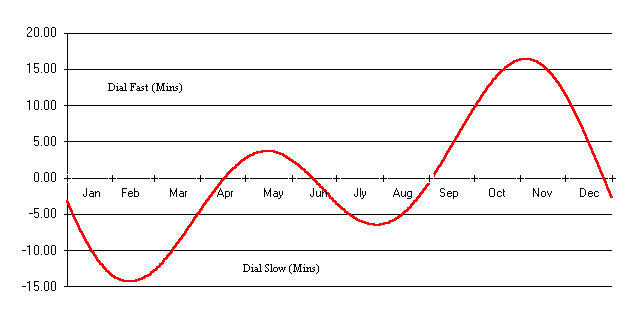
Algunas personas prefieren esta información en tablas en vez de gráficas, por lo que enseguida presentamos dos tablas. Estas son tablas resumidas, que muestran una diferente perspectiva de la Ecuación del Tiempo, y pueden ayudar a recordar algunos puntos claves, por ejemplo, que entre el final de Marzo y mediados de Septiembre, el Sol nunca está más de seis minutos alejado del "tiempo civil", y que para todo Febrero, está trece o catorce minutos ¡más lento! Si desea conocer la Ecuación del Tiempo para cada día del año, existe una tabla en el apéndice A del libro de Waugh.
Tabla que muestra las fechas cuando el "tiempo solar" es casi exactamente un
número entero de minutos más rápido o más lento que el "tiempo civil"
Minutos
(Sol rápido)
16 Nov 11 Oct 27
15 Nov 17 Oct 20
14 Nov 22 Oct 15
13 Nov 25 Oct 11
12 Nov 28 Oct 7
11 Dic 1 Oct 4
10 Dic 4 Oct 1
9 Dic 6 Sep 28
8 Dic 9 Sep 25
7 Dic 11 Sep 22
6 Dic 13 Sep 19
5 Dic 15 Sep 16
4 Dic 17 Sep 13
3 Dic 19 May 4 May 27 Sep 11
2 Dic 21 Abr 25 Jun 4 Sep 8
1 Dic 23 Abr 21 Jun 9 Sep 5
0 Dic 25 Abr 15 Jun 14 Sep 2
(Sol lento)
1 Dic 28 Abr 12 Jun 19 Ago 29
2 Dic 30 Abr 8 Jun 23 Ago 26
3 Ene 1 Abr 5 Jun 29 Ago 22
4 Ene 3 Abr 1 Jul 4 Ago 18
5 Ene 5 Mar 29 Jul 9 Ago 12
6 Ene 7 Mar 26 Jul 18 Ago 4
7 Ene 9 Mar 22
8 Ene 12 Mar 19
9 Ene 15 Mar 16
10 Ene 18 Mar 12
11 Ene 21 Mar 8
12 Ene 24 Mar 4
13 Ene 29 Feb 27
14 Feb 5 Feb 19
Tabla que muestra la Ecuación del Tiempo los días 5, 15 y 25 de cada mes (en minutos y segundos) y el cambio promedio diario en segundos. El signo + significa que el "tiempo solar" es más rápido que el "tiempo civil"
Ecuación del Cambio promedio
Tiempo del día: 5 15 25 (segundos)
Enero -5 min 03 -9 min 10 -12 min 12 20
Febrero -14 min 01 -14 min 16 -13 min 18 5
Marzo -11 min 45 -9 min 13 -6 min 16 16
Abril -2 min 57 +0 min 14 +1 min 56 18
Mayo +3 min 18 +3 min 44 +3 min 16 4
Junio +1 min 46 -0 min 10 -2 min 20 16
Julio -4 min 19 -5 min 46 -6 min 24 20
Agosto -5 min 59 -4 min 33 -2 min 14 11
Septiembre +1 min 05 +4 min 32 +8 min 04 20
Octubre +11 min 20 +14 min 01 +15 min 47 13
Noviembre +16 min 22 +15 min 28 +13 min 11 10
Diciembre +9 min 38 +5 min 09 +0 min 13 27
La Ecuación del Tiempo
Por Art Carlson . Octubre de 1995 .
La rotación de la Tierra actúa como un buen reloj, porque para fines prácticos, es constante. Desde luego, los científicos no son prácticos y se preocupan de que la duración del día se incrementa un segundo cada 40,000 años. Para el resto de nosotros el problema es encontrar una forma conveniente de determinar como está ubicada la Tierra en el espacio. Las estrellas podrían ser una buena referencia, pero son muy tenues (y son muchas) en la noche y desaparecen durante el día. Una valiosa ayuda es el Sol, que está muy a la vista cuando estamos despiertos y que difícilmente pasa inadvertido. Desgraciadamente, la aparente posición del Sol está determinada no sólo por la rotación de la Tierra sobre su eje, sino también por su movimiento de traslación alrededor del Sol. Me gustaría explicar exactamente cómo es que esto afecta y qué se puede hacer al respecto.
El diámetro del Sol tal como se ve desde la Tierra es de 1/2 grado, por lo tanto cada minuto se mueve su propio radio (1/4 grado).
24 horas 60 minutos 1
---------- x ---------- x - grado = 1 minuto
360 grados 1 hora 4
Esto significa que será difícil leer un reloj de Sol con más precisión de un minuto, aunque tampoco nos molestamos en ajustar nuestros relojes a más de esa precisión. Desgraciadamente, si definimos al segundo como medida constante (es decir, la fracción de 1/31 556 925. 9747 del año 1900, que corresponde al "segundo efemérico"), encontramos que algunos días (de mediodía a mediodía) tienen más de 86,400 segundos y otros tienen menos. Por ejemplo, el día solar de Navidad, dura 86,430 segundos. La discrepancia entre "el tiempo aparente" y el "tiempo medio" puede ser hasta +/- 15 minutos. ¿Cómo ocurre esto?.
La inclinación de la eclíptica
Primero hay que considerar que la Tierra gira una vez sobre su eje no en 24 horas, sino en 23 horas 56 minutos 4 segundos. Esto es, que en el curso de un año de 365 días, la Tierra debe girar un tiempo adicional para completar su órbita alrededor del Sol.
1 día 24 horas 60 minutos
----- x ---------- x ---------- = 3 minutos 56 segundos
366 1 día 1 hora
El problema surge porque estos 3 minutos 56 segundos son solo un valor promedio. Imagine un observador sentado en el Polo Norte en una plataforma que gira una vez cada 23 horas 56 minutos 4 segundos. Él verá a las estrellas como fijas y al Sol moviéndose en un círculo. Al plano de este círculo se le llama "eclíptica" y está inclinado 23.45 grados en relación con el plano del Ecuador. El observador verá al Sol moviéndose desde el horizonte hasta 23.45 grados y después regresar al horizonte. El Sol se moverá a velocidad constante (estoy mintiendo, pero aclararé después) a lo largo de su círculo, pero la sombra proyectada en el Polo Norte (por aquel poste con franjas rojas y blancas como caramelo) no se moverá a velocidad constante. Cuando el Sol está cerca del horizonte debe elevarse a un ángulo de 23.45 grados, de manera que tiene que moverse 1.09 grados antes de que la sombra se mueva 1 grado.
1°
------------ = 1.0900°
cos(23.45°)
Por otra parte, a la mitad del verano el Sol está alto en el cielo siguiendo un camino más corto, de manera que debe moverse sólo 1 grado a lo largo de su círculo para que la sombra se mueva 1.09 grados. En primavera y en otoño los 3 minutos 56 segundos se reducen por el factor de 1.09 a 3 minutos 37 segundos, mientras que en verano y en invierno se incrementan a 4 minutos 17 segundos. De esta forma un reloj de Sol puede ganar o perder hasta 20 segundos/día debido a la inclinación de la eclíptica, dependiendo de la época del año. Si el reloj de Sol es preciso en un día determinado, seis semanas después habrá acumulado un error máximo de 10 minutos.
20 segundos 2 1 minuto
----------- x 45 días x --- x ----------- = 10 minutos
1 día pi 60 segundos
La corrección estacional se conoce como "Ecuación del Tiempo" y obviamente debe tomarse en cuenta si queremos que nuestro reloj de Sol tenga la exactitud cercana a un minuto.
Si el estilete o gnomon (el objeto que proyecta la sombra), no es una línea sino un punto (por ejemplo, un orificio en una placa), la sombra (o punto de luz) trazará una curva en el transcurso de un día. Si la sombra se proyecta en una superficie plana, esta curva será (generalmente) una hipérbola, puesto que el círculo del movimiento del Sol junto con el punto del estilete define un cono, y un plano que intersecta un cono forma una sección cónica (hipérbola, parábola, elipse o círculo). En los equinoccios de primavera y otoño, el cono degenera a un plano y la hipérbola a una línea. Con una hipérbola diferente para cada día, se pueden marcar las horas en cada una, lo que implica realizar algunas correcciones. Desgraciadamente, cada hipérbola corresponde a dos días diferentes, uno en la primera mitad y otro en la segunda mitad del año, y estos dos días requerirán de correcciones diferentes. Un compromiso conveniente es dibujar la línea para el "tiempo medio" y añadir una curva mostrando la posición exacta de la sombra al mediodía durante el transcurso del año. Esta curva tomará la forma de la figura de un ocho alargado y se conoce como "analema". Comparando el analema con la línea del mediodía medio, se puede determinar la corrección que deberá aplicarse en ese día. En el equinoccio, encontramos que el día solar es más cercano al día sideral que el promedio de los demás días, es decir, es más corto, de manera que el reloj de Sol es más rápido. Esto significa que en otoño y primavera el tiempo correcto será más temprano que el que la sombra indica, en un valor dado por la curva (será mediodía antes de que el Sol llegue a la línea de las doce del reloj de Sol). En verano y en invierno el tiempo correcto será posterior al indicado (será mediodía después de las 12 en el reloj de Sol).
La excentricidad de la órbita de la Tierra
Si usted observa la figura del ocho calculada correctamente, notará que la parte de la curva correspondiente al otoño y al invierno es un poco más larga que la parte correspondiente a la primavera y al verano. Esto se debe a la mentira que le dije anteriormente. En realidad la Tierra no gira a velocidad constante alrededor del Sol. El 2 de Enero la Tierra está 1.7% más cercana al Sol que el promedio, de manera que la velocidad angular es 3.4% mayor (conservación del momento angular). Esto hace que el día solar sea mayor que el día sideral aproximadamente 8 segundos más que el promedio,
3 minutos 56 segundos
--------------------- x 0.034 = 8.0 segundos/día
1 día
por lo que debido a la excentricidad de la orbita de la Tierra, en el transcurso de tres meses un reloj de Sol acumula un error de 8 minutos.
8.0 segundos 2 1 minuto
------------ x 91 días x --- x ------------ = 8 minutos
1 día pi 60 segundos
En el equinoccio de primavera el tiempo correcto será posterior al que la sombra indique y anterior en el equinoccio de otoño. Esto desplaza las fechas en las que el reloj de Sol es exacto desde los equinoccios hacia el verano, haciendo menor la curva del ocho en la parte correspondiente al verano.
El error de 20 segundos por día debido a la inclinación de la eclíptica y el error de 8 segundos por día debido a la excentricidad, actúan en la misma dirección alrededor de la época de Navidad y suman casi exactamente los 30 segundos por día mencionados anteriormente. Los errores acumulados de 10 minutos y 8 minutos debido a estos dos efectos no se suman directamente, de manera que el error máximo acumulado es poco menos de 18 minutos. Si calcula todo correctamente, encontrará que durante el transcurso de un año, un reloj de Sol será 16 minutos 23 segundos más rápido (el 3 de Noviembre) y hasta 14 minutos 20 segundos más lento (el 12 de Febrero).
Suponga que en Octubre usted inicia un receso de 15 minutos a las 10:45 hora civil. Si confía en el reloj de Sol afuera de su edificio sin tomar en cuenta la Ecuación del Tiempo, será tarde para la sesión de las 11:00 apenas haya cruzado la puerta.
Si usted conoce otras direcciones, apreciaremos nos envíe un mensaje por correo electrónico. Gracias.
|
Para una vista completa de Relojes de Sol en Internet oprima aquí |
|
Esta versión es una traducción de la página en inglés, realizada por José C. Montes J. y Martha A. Villegas V. de Torreón, Coahuila, México, el 7 de Febrero del 2000. Este sitio es diseñado y mantenido por Internetworks Ltd de Epsom, Inglaterra |
|
www.sundials.co.uk/equation.htm colocado por primera vez en 1996. Ultima revisión el 25 de Abril de 1999 |
|
Comentarios/ sugerencias/ problemas, por favor comuníquese con el Webmaster |

